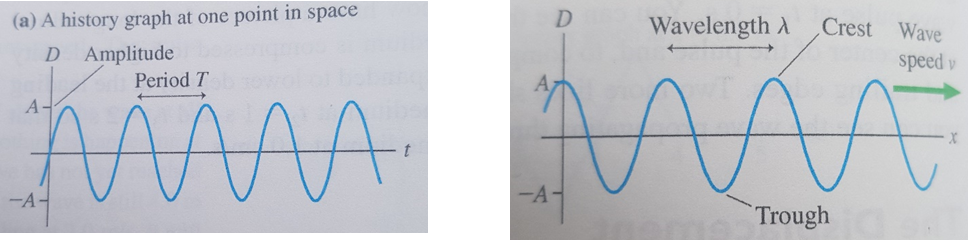Don’t forget to Subscribe to support my work!
Introduction
Binary can represent sound, images and characters. In this article we are going to be solely focusing on sound. The reason being is because there are clear links in this topic with Computer Science and Physics.
The topic discussed in this article will be how binary is used to represent sound. The sub topics will involve sampling, the Nyquist Theorem, amplitude and other aspects in relation to sound. Computer process data in a digital form using microprocessors also referred to as “chips”. A chip is a small circuit which receives electronic pulses. It is these pulses of electricity which allow a computer to represent text, images, audio, numbers and sound. Before we do this, it is a good idea to also go into the topic of waves.
Binary – What is it?
Data is made up of raw facts and figures and can be represented in many different forms including text, numbers, pictures, sounds and video clips. Information can be derived from data when it is processed. Numbers are represented in the following ways: Denary; Binary; Hexadecimal; and Octal. We will be focusing solely on binary. Binary is a number system with base 2. It counts in the multiples of 2.
A bit is a single Binary Digit. A processor can only recognise if it is receiving an electronic signal or if it is not. This is represented as either a 1 or a 0. The computer strings these 0’s or 1’s together. Binary can be represented in three different ways: images; sound; and characters. For this article we will be focusing solely on sound.
Waves
Waves are used to transfer energy or to carry information. In this case of Computer Science, waves are used for carrying TV or phone channels around the globe via satellite links. The different types of waves in Physics are sound waves, electromagnetic waves, seismic waves and water waves. In the case of Computer Science, we just want to focus on sound waves as sound is one form of binary representation. Waves can be classified as transverse and longitudinal.
Sound waves are longitudinal waves. Sound waves are vibrations in a medium that travel through the medium. When a human speaks, the vocal cords make the surrounding air vibrate and the vibrations spread out. Sound waves travel faster than solids and liquids than through air. A loudspeaker supplied with alternating current (AC) creates sound waves. The reason for this being the case is because the diaphragm of the loudspeaker is forced to move to and from. The diaphragm compresses the surrounding air in front of it as it moves forwards. The diaphragm moves back before creating another compression. The air vibrates to and fro as the sound waves pass through it.
Sound
An object vibrating in air creates sound waves in the surrounding air because the surface of the vibrating object pushes and pulls on the air. Sound waves are longitudinal.
The image shows sound from a microphone to the speaker
Analogue signals representing the sound are coded into digital data which the computer can store as a sequence of bits. This is called the ADC or analogue to digital converter. An ADC is needed in many modern measuring instruments as the reading is frequently displayed digitally but, the input from say a transducer measuring temperature is in analogue form (Duncan, 1997).
A 16-bit ADC is sufficient to give CD quality sound. To input sound the sound wave must be sampled at regular intervals. The greater the rate of sampling, the more accurate the sound stored. However, this also increases the amount of memory needed to store the sound. ADC is also used with any analogue sensor. Digital data representing the sound is used to create a analogue signal, passed through the amplifier and played on the speakers.
We can also get a DAC, which is a Digital-to-Analogue Converter.
Sampling
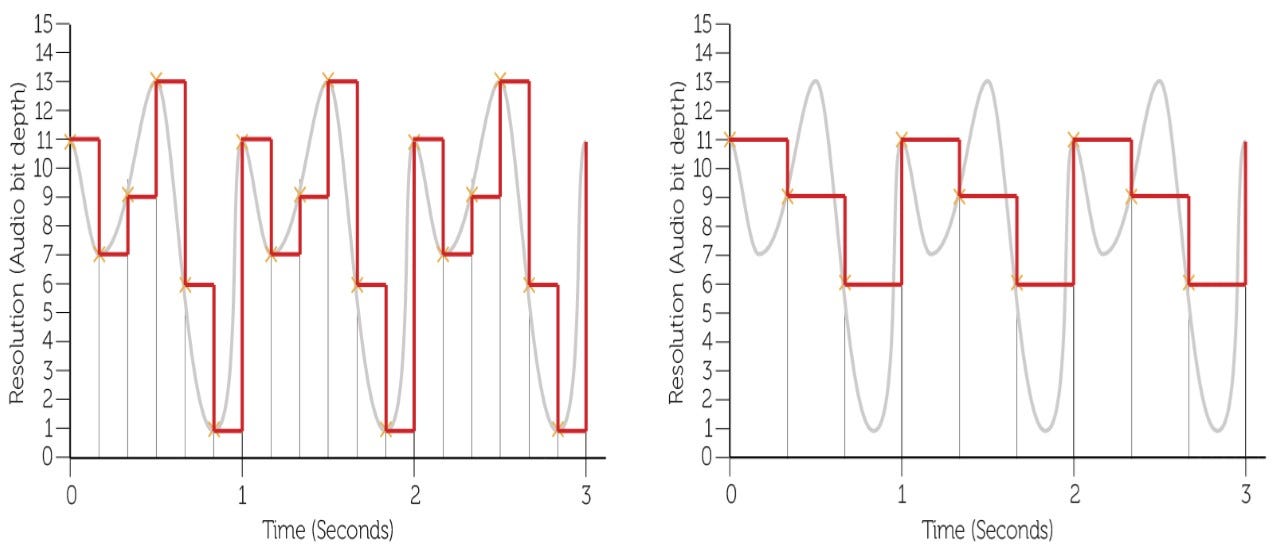
A computer system is only able to store and process binary digits, as it is a digital device. Sound is an analogue signal. If an analogue signal, such as sound, is sent to a computer system, it has to be converted into a digital signal before it can be processed. Sound is converted into a digital signal by a process called sampling. This is where hardware, such as a microphone, measures the level of sound many times per second and records this as binary digits.
The most common sampling rate for music is 44,100 samples per second, which is 44,100 Hz (=44.1 kHz). A Voice over Internet protocol (VoIP) has a sampling rate of 8 kHz, which is enough for human voice to be heard clearly but the quality is reduced to certain extent. The frequency or sample rate per second affects the level of detail in the digital representation. The greater the frequency, the greater the accuracy, and file size.
The bit depth is the number of bits available for each sample. The higher the bit depth, the higher the quality the audio will be. A CD has a bit depth of 16 bits and a DVD has a bit depth of 24 bits. An n bit system can have 2n different values. Hence, a CD can represent values from 0 to 65535(216 -1). High-quality audio files are created as pulse-code modulation (PCM). PCM is the process for digitising a sound file and creating an uncompressed file. WAV and AIFF are a few examples of uncompressed audio file formats.
The Bit Rate
The Bit rate is the number of bits of data used to store data sampled every second. The unit for bit rate is kilobits per second (kbps):
Bit rate=Sampling rate × bit depth × channels
An audio file has 44,100 samples per second, bit depth of 16-bits and 2 channels (stereo audio). Bit rate of this file can be calculated as:
Bit rate=44100×16×2=1,411,200 bits per second=1411.2 kbps
A reasonable music audio must have a minimum bit rate of 128 kbps. The more the bit rate the better the quality. This is the reason why audio quality of a music CD is better than downloading from internet.
In relation to bit rate and file size, a three-minute audio file with sampling rate of 44,100 samples per second, bit depth 16 bits and 2 channels, has a bit rate of 1411.2 kbps per second.
For 3 minutes, the number of bits required is, 1,411,200×180=254,016,000 bits. This value is equal to 254016000 ÷ 8 = 31752000 bytes = 31.75 megabytes (MB). This is the file size of three-minute audio file.
Sampling Frequency
Sampling Frequency by definition is the number of times that the sound level is sampled per second. The higher the sampling frequency, the better the quality of the sound recorded. A typical sampling frequency is 44,000 times per second, also known as 44 kHz. This is the sampling frequency used on most audio CDs. Sound sampled at 44 kHz in stereo will produce a large amount of data and as such, this data may need to be compressed. When sound files are compressed, data is removed to reduce the size.
For example:
File size (in bits) = Sample rate (in kHz) x bit depth x length (in seconds)
30 seconds x 8 bits x 500 kHz
120,000 bits
File size = 120,000 bits
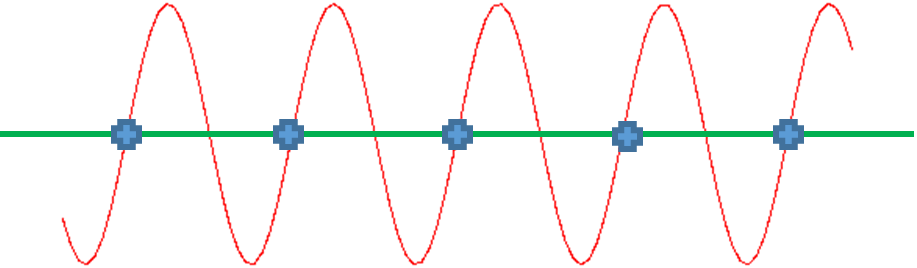
The Nyquist Theorem
In 1928 Harry Nyquist proposed that the sampling frequency should be at least twice the rate of the highest frequency of the signal being sampled.
Harry Nyquist was a Swedish physicist and electronic engineer who made important contributions to communication theory. He worked at AT&T / Bell Telephone Laboratories from 1917 to 1954. Bell Labs patent lawyers wanted to know why some people were so much more productive (in terms of patents) than others. The only thing they found was that:
“… Workers with the most patents often shared lunch or breakfast with a Bell Labs electrical engineer named Harry Nyquist. It wasn’t the case that Nyquist gave them specific ideas. Rather, as one scientist recalled, ‘he drew people out, got them thinking.”
The Nyquist theorem states that in order to have an accurate representation of a signal, the sampling rate has to be at least twice the highest frequency present in the signal:
Sampling Rate = 2 * maximum frequency
Remember that the frequency of a sound wave is determined by the number of wave cycles that occur per second, where a wave cycle is a complete oscillation (up and down) in a sound wave. In a simple signal that consists of only a single sound wave, this can be seen easily. Sampling at double the maximum frequency can keep all the peaks of the original wave (depending on when the samples are taken), and sampling at an even higher frequency can capture the signal variations more accurately.
When an analogue-to-digital or digital-to-analogue converter is applied in a complete system using digital signal processing, extra components must be added. We can have sampling with no-aliasing, sampling with aliasing and sampling with quantisation errors. We can also have the Nyquist Pulse and Square-Root Nyquist Pulse. (Van De Plasshe, 2003; Skalar, 2001)
What Wave is Sound?
Sound is a sine wave. A sine wave is a geometric waveform that oscillates (moves up, down, or side-to-side) periodically. The reason why a sine wave is called a sine is because it is generally plotted or based on the trigonometric sine function.
If we sample at 1 time per cycle, we can think it's a constant like the one below:
If we sample at 1.5 times per cycle, we can think it's a lower frequency sine wave like the one below:
Now if we sample at twice the sample frequency, i.e Nyquist Rate, we start to make some progress. We get a sawtooth wave that begins to start crudely approximating a sine wave like the one below:
Another type of wave is called a sinusoidal wave. A sinusoidal wave is a wave that oscillates with simple harmonic motion (SHM). For example, we can have a loudspeaker cone that oscillates in SHM that will radiate a sinusoidal sound wave. The sinusoidal electromagnetic waves broadcast by television and FM radio stations are generated by electrons oscillating back and forth in the antenna wave with SHM.
Above are two examples of sinusoidal waves (Knight, 2017). The reason for adding sinusoidal waves is so the reader knows the difference between sinusoidal and sine waves and therefore doesn’t get the two mixed up.
Mono or Stereo?
There is one final factor that influences audio file size: whether a sound is monophonic or stereophonic. Mono sound is just one track of sound. Stereo sound contains two different tracks to add an impression of positioning and direction to the recording. As you might expect, needing two tracks doubles the storage space required. A stereo recording has twice the file size of a mono recording of the same duration, sampling rate, and sample resolution. To find the storage requirements for an audio file in bits, you need to:
· calculate the number of samples by multiplying the sampling rate in Hz (samples/second) by length of the sound recording in seconds
· calculate the number of bits by multiplying the number of samples by the sample resolution (bits/sample)
storage requirements (in bits) = sampling rate × seconds × sample resolution
If you have to express the answer in a different unit of measurement, you will need to do further calculation(s). For a stereo file, the only difference in the equation is another factor of 2 that takes into account the use of two tracks:
stereo storage requirements (in bits) = sampling rate × seconds × sample resolution × 2
Audio compression removes frequencies and sounds which we can’t hear or detect. A soft quiet frequency when something louder is playing at the same time. There are other formats.
Sound Synthesis
Another aspect of sound is synthesising sound. Sound synthesis is the use of electronic devices for creating sound. The final audible sounds will be generated using analogue techniques but, digital methods can be used to transmit the sound before the final stage. In creating sound from scratch, it is common to start from pure waveforms and modify these to mimic the characteristics of sound. There are some common methods to sound synthesis (British Computer Society. Glossary Working Party, 2005).
Modulation is one such method. Modulation by definition is a term that refers to changes made in a carrier according to the information being sent. We need modulation as it performs two basic functions. Modulation allows a signal to be moved to a different part of the frequency spectrum and it allows a number of different signals to be send simultaneously over the same channel (Comer, 2005).
To understand its importance let us consider the transmission of a simple speech signal. A signal must cover a frequency range from about 300 Hz to about 3 kHz. In the diagram, this corresponds to the VF band of the radio frequency spectrum. Possible method of communication would be to connect our signal to a suitable antenna and broadcast the signal as a radio wave. This isn’t an attractive option.
Laws of electromagnetic propagation dictates the size of the antenna must be a significant fraction (perhaps a quarter) of the wavelength of the transmitted signal. To transmit a signal with frequency components down to 300 Hz, we would need an antenna approximately 250 km in length. Modulation addresses this issue by translating our signal to a higher frequency. We can combine our signal with one at a much higher frequency. We are then able to translate our signal to another part of the frequency spectrum. By using this technique to move our signal so that its lowest frequency components are at 300 MHz rather than 300 Hz, our antenna needs to be 25 cm long rather than 250 cm long.
Modulation can be divided into a number of basic forms:
· Analogue Modulation
o Frequency Modulation
o Amplitude Modulation
· Digital Modulation
o Amplitude-Shift Keying
o Frequency-Key Shifting
o Phase-Key Shifting
· Pulse Modulation
o Pulse-Amplitude Modulation (PAM)
o Pulse-Width Modulation (PWM)
o Pulse-Position Modulation (PPM)
o Pulse-Code Modulation (PCM)
We are not going to go into them all as the article is quite long as it is.
The Musical Instrument Digital Interface (MIDI) a technical standard that describes a communications protocol, digital interface, and electrical connectors that connect a wide variety of electronic musical instruments, computers, and related audio devices for playing, editing, and recording music. MIDI records the information about each note. It is also time sequenced and attempts to recreate that note when played. MIDI also uses less disk space and can send event messages to other instruments (volume changes, Sync Tempo). The metadata stored for each note (Duration, Instrument, Volume, Channel ……) can be edited and manipulated. The quality depends on the quality of the synthesiser.
MIDI uses event messages to control various properties of the sound. These messages are typically encoded in binary and provide communication between MIDI devices or between a MIDI device and the processor. For example, on a MIDI keyboard, an event message may contain data on:
· when to play a note
· when to stop playing the note
· timing a note to play with other notes or sounds
· timing a note to play with other MIDI-enabled devices
· what pitch a note is
· how loud to play it
· what effect to use when playing it
The advantages of using midi files over other digital audio formats are MIDI files tend to be much smaller. This means they require less memory and also load faster, which is particularly advantageous if the MIDI file is embedded in a web page. They are completely editable as individual instruments can be selected and modified. MIDI supports a very wide range of instruments providing more choices for music production. MIDI files can produce very high quality and authentic reproduction of the instrument.
With this system the full sound signal does not need to be transmitted, only the instructions to play the sound need to be transmitted as ‘event messages’. It is up to the instrument to create the sound, so the instrument can be changed using the same messages for a different sound. MIDI messages are usually only 2 or 3 bytes long which significantly reduces the amount of data transferred. As sounds are synthesised, they may be less realistic but since no data is lost about musical notes, the quality can be higher. A sound processor can be linked to several instruments or computers. This can send a timed sequence of event messages to:
· Synchronise tempo
· Control pitch
· Change volume
· Introduce and silence other instruments in a digital orchestra
Other devices are sound controller, sound generator and a music synthesiser. That concludes this long snapshot of the physics and electronics in relation to representation of sound in binary.
Reference List
Bradley, R. (1999) Understanding Computer Science to Advanced Level Fourth Edition Cheltenham: Stanley Thornes (Publishers) Limited
Breithaupt, J. (2003) Physics Second Edition Basingstoke: Palgrave Macmillan
British Computer Society. Glossary Working Party, (2005) The BCS Glossary of ICT and Computing Terms Eleventh Edition Harlow, Essex: Pearson Education Limited
Comer, D. E. (2015) Computer Networks and Internets Sixth Edition Global Edition Harlow Essex: Pearson Education Limited
Duncan, T. (1997) Success in Electronics 2nd Edition London: Hodder Education
Englander, I. (2014) The Architecture of Computer Hardware, Systems Software and Networking An Information Technology Approach Fifth Edition, Hokoben, New Jersey: John Wiley and Sons Inc
Knight, R. D. (2017) Physics for Scientists and Engineers A Strategic Approach with Modern Physics Harlow, Essex: Pearson Education Limited
Sklar, B. (2001) Digital Communications Fundamentals and Applications Second Edition New Jersey: Prentice-Hall Inc.
Van De Plassche, R. (2003) CMOS Integrated Analog-to-Digital and Digital-to-Analog Converters 2nd Edition Dordrecht: Kluwer Academic Publishers
Any questions please drop a comment below. If you like the sound of my work, please share and subscribe!